2.5. Булийн макстерм илэрхийлэл

Үнэмшлийн хүснэгтээс Булийн минтерм илэрхийллийг олж болохоос гадна булийн макстерм илэрхийллийг гаргаж болно.

Жишээ нь 3 оролттой 1 гаралттай комбинацийн хэлхээний үнэмшлийн хүснэгт өгөгдсөн байг.

Үнэмшлийн хүснэгтнээс гаралт 0 байх гаралтуудыг сонгож авна.

Энд гаралт 0 байх 2 тохиолдол байгаа бөгөөд эхний гаралт нь оролтын 100 байх хувилбарт таарч байна. Тэгвэл оролтын ямар хувилбарт нийлбэр нь 0 байх илэрхийллийг олно. Өөрөөр хэлбэл ямар үед бүгд 0 байх илэрхийллийг олно.

Мөн дараагийн 0 байх гаралт нь оролтын ямар хувилбарт таарч байгаа ажиглаж оролтын нийлбэр 0 байх илэрхийллийг олно.

Ингээд 0 байх гаралт тус бүрийн хувьд оролтын нийлбэр 0 байх хувилбарыг олж хооронд үржих замаар product of sum /нийлбэрүүдийн үржвэр/ гэж нэрлэгддэг Булийн макстерм илэрхийллийг олно.

Булийн макстерм илэрхийллийг олсноор OR-AND логик хэлхээг байгуулах боломжийг олгодог. Дээрх жишээний хувьд OR-AND логик хэлхээг зурвал:

Жич: анхаар! Булийн макстерм илэрхийллийг OR-AND хэлхээгээр дүрсэлж болно. Гэхдээ Булийн макстерм илэрхийллийг цаашид энэ хичээлд заасан зааврын дагуу олохгүй. 3-р сэдэвт хэрхэн хялбарчлах талаар үзэх ба 2-6 хүртэл оролттой хэлхээг Карногийн тор ашиглан хэрхэн хялбарчлах талаар үзэх тул цаашид зөвхөн Булийн хялбарчлагдсан макстерм илэрхийллээр л OR-AND логик хэлхээг байгуулах ёстойг санах хэрэгтэй!

Хэрэв 6-гаас дээш оролттой хэлхээ таарвал Карногийн тор ашиглан хялбарчлах боломжгүй бөгөөд энэ тохиолдолд хэрхэн хялбарчлахыг сүүлд үзэх болно.

2.4. Булийн минтерм илэрхийлэл

Комбинацийн хэлхээ нь оролтоос хамаарч гаралт нь шууд өөрчлөгддөг хэлхээг ойлгоно.

Иймээс комбинацийн хэлхээ нь оролтын бүх боломжит утгуудад гаралт ямар байхыг харуулсан үнэмшлийн хүснэгт хэлбэрээр өгөгдөнө.

Жишээ нь А, В, С гэсэн 3 оролттой Y гэсэн нэг гаралттай комбинацийн хэлхээг авч үзье. 3 оролттой тул оролтын нийт 8 боломж байна. Эдгээр боломж тус бүрд гаралтын утга ямар байхыг харуулсан хүснэгтийг энэ хэлхээний үнэмшлийн хүснэгт гэнэ.

Энэ хүснэгтнээс гаралтын Булийн минтерм илэрхийлэл буюу sum of product /үржвэрийн нийлбэр/ илэрхийллийг олъё.

Үүний тулд эхлээд 1 гарч буй гаралтуудыг тэмдэглэнэ. Энэ жишээнд нийтдээ 2 ширхэг гаралт 1 байх гаралт байна.

Эхний 1 нь оролт АВС-гийн утга 001 байх үед гарсан байна. Тэгвэл энэ 3 оролт ямар байвал үржвэр нь 1 гарах вэ гэдгийг олно. Энэ тохиолдолд А-гийн үгүйсгэл, В-гийн үгүйсгэл С 3-ийн үржвэр байх буюу А’B’C үед гаралт 1 болохыг оролтоос харж болно.

Үүнтэй адилаар үүний дараагийн 1 нь оролт АВС-гийн утга 111 байх үед таарч байна.

Ингээд гаралт бол энэ 2 боломит утгын нийлбэр байна.

Булийн минтерм илэрхийллийг AND-OR логик хэлхээгээр дүрсэлж болно.

Жич: анхаар! Булийн минтерм илэрхийллийг AND-OR хэлхээгээр дүрсэлж болно. Гэхдээ Булийн минтерм илэрхийллийг цаашид энэ хичээлд заасан зааврын дагуу олохгүй. 3-р сэдэвт хэрхэн хялбарчлах талаар үзэх ба 2-6 хүртэл оролттой хэлхээг Карногийн тор ашиглан хэрхэн хялбарчлах талаар үзэх тул цаашид зөвхөн Булийн хялбарчлагдсан минтерм илэрхийллээр л AND-OR логик хэлхээг байгуулах ёстойг санах хэрэгтэй!

Хэрэв 6-гаас дээш оролттой хэлхээ таарвал Карногийн тор ашиглан хялбарчлах болмжгүй бөгөөд энэ тохиолдолд хэрхэн хялбарчлахыг сүүлд үзэх болно.

2.3. ДеМорганы теорем

Нийлбэрийн гүйцээлт нь тус бүрийн үгүйсгэлийг хооронд нь үржсэнтэй тэнцүү байдаг.

Үүнтэй адилаар үржвэрийн гүйцээлт нь тус бүрийн үгүйсгэлийг хооронд нэмсэнтэй тэнцүү байдаг.

Үүнийг ДеМорганы теорем гэдэг бөгөөд үүнийг үнэмшлийн хүснэгтийг байгуулах замаар шалгаж болно.

ДеМорганы теоремыг анхааралтай харвал зурагт үзүүлсэн зүйлийг харж болно.

Энд зураг дээр NOR гейтийн 2 боломжит симболыг харуулж байна. Өөрөөр хэлбэл NOR гейтийг дээрх 2 тэмдэглэгээний алинаар нь ч тэмдэглэж болно.

Үүнтэй адилаар NAND гейтийг ДеМорганы теорем ёсоор мөн 2 янзаар тэмдэглэхийг зөвшөөрдөг. Үүнд:

ДеМорганы теорем нь NAND болон NOR гейтийг универсаль элемент болохыг харуулдаг.

Бид нь өмнө нь үндсэн 2 хэлбэрийн логик хэлхээ байдаг гэж үзсэн. Үүнд AND-OR логик хэлхээ ба OR-AND логик хэлхээ.

Тэгвэл AND-OR логик хэлхээг универсаль NAND элементээр хийж NAND логик хэлхээг байгуулах боломжтой байдаг. AND-OR логик хэлхээг хэрхэн NAND логик хэлхээ болгон хувиргахыг зурагт харуулав.

Энд үгүйсгэлийг дангаараа байвал А оролтонд хэрэглэсэн NAND гейтийг ашиглаж орлуулна.

NAND логик хэлхээг байгуулахдаа дараах дүрмийг баримтлана.

·         Эхлээд AND-OR хэлхээг байгуулна.

·         AND элементийн гаралтанд нүхтэй бөмбөлөг тавьж NAND болгоно.

·         OR элементийн оролтуудыг нүхтэй бөмбөлөгтэй болгож NAND болгоно.

·         Ингэхдээ давхар үгүйсгэл хэвээрээ байдаг гэдэг дүрмийг баримтлах ба дан үгүйсгэл орсон бол дахин нэг үгүйсгэлийг нэмж хэрэглэх замаар үгүйсгэл зөв хэрэглэгдсэн эсэхийг шалгана.

Үүнтэй адилаар ДеМорганы теоремыг ашиглан OR-AND логик хэлхээг универсаль NOR логик хэлхээгээр сольж болно. Жишээ болгон нэг OR-AND хэлхээг хэрхэн NOR логик хэлхээ болгон хувиргахыг харуулья.

Ингэхдээ дараах дүрмийг баримтлана.

·         Эхлээд OR-AND хэлхээг байгуулна.

·         OR элементийн гаралтанд нүхтэй бөмбөлөг тавьж NOR болгоно

·         AND элементийн оролтуудыг нүхтэй бөмбөлөг тавьж NOR болгоно.

·         Давхар үгүйсгэл хэвээрээ байна гэдэг дүрмийг баримтлан үгүйсгэлийг зөв хэрэглэсэн эсэхийг шалгана.

2.2. Бусад логик гейтүүд

Үндсэн 3 гейтээс гадна NAND, NOR, XOR, XNOR гейтүүд өргөн хэрэглэгддэг бөгөөд эдгээр гейтүүдтэй товч танилцая.

NAND гейт нь логик AND гейтийн гаралтанд үгүйсгэгч ашиглах бөгөөд түүний хэлхээний симболыг харуулбал:

Жич : үгүйсгэгчийг цаашид ихэнхдээ дундаа нүхтэй бөмбөлгөөр дүрслэх болно. Өөрөөр хэлбэл дундаа нүхтэй бөмбөлгийг үгүйсгэгч буюу NOT гейт байгаагаар төсөөлнө.

2 оролттой NAND гейтийн ажиллагааг тайлбарлах үнэмшлийн хүснэгт нь дараах хэлбэртэй байна.

Энд complement буюу гүйцээлт гэсэн үйлдлийг дээгүүр зураас эсвэл дээд босоо зураасаар тэмдэглэнэ.

Мөн 3 оролттой NAND гейтийн үнэмшлийн хүснэгтийг байлуулья.

OR гейтийн гаралтанд NOT гейтийг хослуулан хэрэглэсэн гейтийг логик NOR гейт гэнэ.

Логик NOR гейтийн хэлхээний симболыг харуулья.

2 оролттой NOR гейтийн ажиллагааг тайлбарлах үнэмшлийн хүснэгт нь дараах хэлбэртэй байна.

Харин 3 оролттой NOR гейтийн үнэмшлийн хүснэгт бол дараах хэлбэртэй байна.

Логик OR үйлдэл нь аритметикийн нэмэх үйлдэлтэй төсөөтэй тухай ярьсан. Гэвч 1+1=1 гэсэн үйлдэл нь аритметикийн үйлдлээс ялгаатай болохыг харуулдаг. Үнэндээ аритметикийн хувьд 1+1=0 бөгөөд 1 оронг санадаг. Тэгвэл OR гейтийг сайжруулаад илүү нэмэх үйлдэлтэй адилхан болгосон элементийг сайжруулсан OR буюу товчоор XOR, NOR гейтийн сайжруулсан хувилбарыг сайжруулсан NOR буюу XNOR гейт гэж тус тус нэрлэнэ.

2 оролттой сайжруулсан OR болон сайжруулсан NOR-ийн үнэмшлийн хүснэгтийг харуулья.

XOR элементийг хэлхээнд OR-аас арай өөрөөр тэмдэглэх ба XOR үйлдлийг дугуй доторх нэмэхээр тэмдэглэнэ.

XNOR гейтийг XOR-ийн үгүйсгэл хэлбэрээр хэлхээнд тэмдэглэнэ.

Ингээд 3 оролттой XOR ба XNOR гейтүүдийн үнэмшлийн хүснэгтийг байгуулья.

2.1. Үндсэн логик гейтүүд

Тоон электроникийн үндсэн суурь бааз элемент нь логик гейтүүд юм. Логик гейтүүд нь хүчдлийн их эсвэл бага төвшинг хэрэглэнэ. Энэ хичээлийн хүрээнд хүчдлийн их төвшинг бинари 1, хүчдлийн бага төвшинг логик 0 гэж ойлгоно.

Бүхий л тоон системүүд нь зөвхөн үндсэн 3 логик гейт дээр суурилагдсан байдаг. Эдгээр нь логик AND, гейт, логик OR гейт мөн логик NOT гейтүүд болно. Өөрөөр хэлбэл бүхий тоон системүүд нь үнэндээ логик үйлдлүүдийг л гүйцэтгэдэг гэж ойлгож болно.

Бүгд үнэн үед үнэн байдаг, аль нэг нь худал бол худал байдаг логик үйлдлийг AND үйлдэл гэдэг. Тэгвэл энэ үйлдлийг гүйцэтгэдэг логик элементийг AND гейт гэнэ.

Жишээ нь үнэнийг бинари 1-ээр, худлыг бинари 0 гэвэл A ба В гэсэн 2 үзэгдлийн хувьд AND логик үйлдлийг хүснэгтээр тодорхойлъё. Өөрөөр хэлбэл 2 оролттой 2 оролтын боломжит утгуудад гаралт ямар байхыг харуулсан хүснэгтийг зохиоё.

Тэгвэл А, В, С гэсэн 3 оролттой үед мөн эдгээрийн боломжит утгуудад үр дүн болох Z ямар байхыг харуулсан хүснэгтийг зохиоё.

Оролтын бүх боломжит утгуудад гаралт ямар байхыг харуулсан дээрх хүснэгтүүдийг цаашид үнэмшлийн хүснэгт гэнэ.

Хүснэгтнээс харахад логик AND үйлдэл нь аритметикийн үржүүлэх үйлдэлтэй төсөөтэй харагдаж байна. Иймээс логик AND үйлдлийг цаашид үржих тэмдгээр эсвэл байхгүйгээр тэмдэглэнэ. Ингээд логик AND үйлдлийг гүйцэтгэдэг AND гейтийг хэлхээнд хэрхэн тэмдэглэх симболыг 2 оролттой ба 3 оролттой AND гейтийн хувьд зурагт харуулья.

Харин аль нэг нь үнэн бол үнэн, бүгд худал байвал л сая худал байдаг логик үйлдлийг логик OR үйлдэл гэнэ.

2 оролттой тохиолдолд логик OR үйлдлийн үнэмшлийн хүснэгтийг байгуулья.

Мөн 3 оролттой тохиолдолд логик OR үйлдлийн үнэмшлийн хүснэгтийг байгуулья.

Үнэмшлийн хүснэгтээс харахад логик OR үйлдэл нь аритметикийн нэмэх үйлдэлтэй төсөөтэй харагдаж байна. Иймээс цаашид логик OR үйлдлийг нэмэх тэмдгээр тэмдэглэх ба логик OR үйлдлийг гүйцэтгэдэг OR гейтийг схемд дараах байдлаар тэмдэглэнэ.

Жич: үнэндээ OR үйлдэл зарим талаараа л аритметикийн нэмэх үйлдэлтэй төсөөтэй. Жишээ нь 0+1=1 зөв юм шиг байгаа ч 1+1=1 гэсэн үйлдэл нь аримтетикийн нэмэх үйлдлээс өөр байгааг анзаарч болно. Ерөнхийдөө л төсөөтэй болохоос аритметикийн нэмэх, үржих үйлдлүүд ба логик OR, AND үйлдлүүд ялгаатай болохыг байнга санах хэрэгтэй. Жишээ нь логик сигнал нь хүчдлийн ялгаатай 2 төвшинг ашигладаг бөгөөд 2 логик сигналыг хооронд нь нэм эсвэл үрж гэвэл үүнийг хэзээ ч ойлгохгүй. Харин 2 логик сигналын хувьд логик AND эсвэл логик OR үйлдлийг гүйцэтгэ гэвэл маш ойлгомжтой. Иймээс л тоон электроникт хэрэглэгддэг үндсэн үйлдэл бол логик AND, OR эсвэл NOT үйлдэл л байна.

NOT гейтийг заримдаа инвертер буюу үгүйсгэгч ч гэж нэрлэдэг. Логик NOT үйлдлийг гүйцэтгэдэг NOT гейтийн үнэмшлийн хүснэгт болон логик симболыг зурагт харуулав.

Жич: NOT гейтээр гүйцэтгэгдэх үйлдлийг цаашид complement буюу гүйцээлт гэж нэрлэнэ. Өөрөөр хэлбэл тоон электроникт үгүйсгэгч гэсэн ойлголт байдаггүй. 0-ийн гүйцээлт 1, 1-ийн гүйцээлт 0, 01-ийн гүйцээлт бол 10, 010110110-ийн гүйцээлт бол 101001001 гэсэн ойлголт л байдаг. Өөрөөр гүйцээлт гэдэг үйлдлийг гүйцэтгэдэг элемент бол NOT гейт гэж ойлгоно. Энэ талаар цаашдаа 1-ийн гүйцээлт, 2-ийн гүйцээлт гэсэн сэдэвт тодорхой өгүүлэх болно.

Эдгээр логик гейтүүдийг ихэвчлэн хооронд нь хослуулан хэрэглэх бөгөөд практикт өргөн хэрэглэгддэг логик гейтүүдийн хослолын үндсэн 2 хэлбэр нь AND-OR хэлхээ ба OR-AND хэлхээнүүд болно.

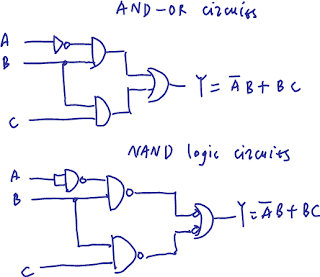
Логик AND-OR хэлхээ нь эхлээд оролтуудын хувьд логик AND үйлдлийг гүйцэтгээд гарсан үр дүнгүүдийн хувьд OR үйлдэл гүйцэтгэхийг ойлгоно. Доорх жишээнд Y=AB+BC үйлдлийг гүйцэтгэх хэлхээг үзүүлсэн болно. Y=AB+BC илэрхийллийг sum of product /үржвэрүүдийн нийлбэр/ буюу товчоор Булийн минтерм илэрхийлэл гэж нэрлэнэ.

Энэ хэлхээ нь А, В, С гэсэн гурван оролттой учраас энэ хэлхээний үнэмшлийн хүснэгт нь дараах хэлбэртэй байна.

Логик OR-AND хэлхээ нь эхлээд оролтуудын хувьд логик OR үйлдлийг гүйцэтгээд гарсан үр дүнгүүдийн хувьд логик AND үйлдлийг гүйцэтгэнэ. Доорх жишээнд Y=(A+B)(B+C) үйлдлийг хэрхэн гүйцэтгэхийг харууллаа. Y=(A+B)(B+C) илэрхийллийг цаашдаа product of sum /нийлбэрүүдийн үржвэр/ буюу товчоор Булийн макстерм илэрхийлэл гэж нэрлэнэ.

Энэ хэлхээ нь А, В, С гэсэн гурван оролттой учраас энэ хэлхээний үнэмшлийн хүснэгт нь дараах хэлбэртэй байна.

Жич: бид цаашдаа энэ 2 төрлийн хэлхээнээс AND-OR хэлхээг өргөн хэрэглэх болно.